Two urns contain white balls and yellow balls, setting the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. This analysis delves into the concepts of probability and conditional probability, exploring the intricacies of drawing balls from urns and the fascinating relationships that emerge.
The contents of the urns, the distribution of balls, and the formulas for calculating probabilities are meticulously described, providing a solid foundation for understanding the subsequent analysis.
Two Urns Containing White and Yellow Balls: Two Urns Contain White Balls And Yellow Balls
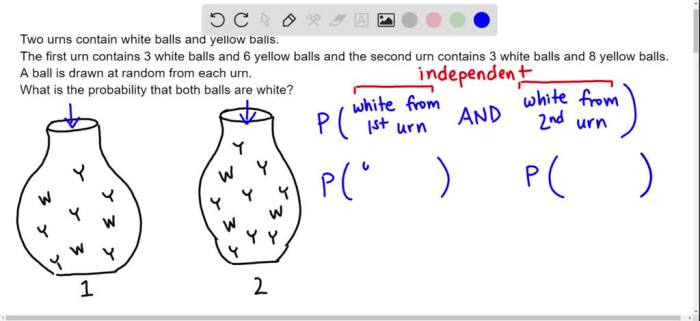
In this analysis, we consider two urns, each containing a mixture of white and yellow balls. Our objective is to determine the probability of drawing balls of specific colors from these urns and to explore the concept of conditional probability in this context.
Urn Contents
Urn 1:Contains 10 balls, of which 6 are white and 4 are yellow.
Urn 2:Contains 15 balls, of which 9 are white and 6 are yellow.
Probability Calculations, Two urns contain white balls and yellow balls
The probability of drawing a specific color ball from an urn is calculated using the following formula:
P(drawing a white ball) = Number of white balls / Total number of balls
For Urn 1, the probability of drawing a white ball is 6/10 = 0.6.
For Urn 2, the probability of drawing a yellow ball is 6/15 = 0.4.
Conditional Probability
Conditional probability refers to the probability of an event occurring given that another event has already occurred. In our scenario, we can consider the probability of drawing a specific color ball from an urn given that we have already drawn a ball of a different color.
Comparison of Urns
The following table compares the probabilities of drawing white and yellow balls from Urn 1 and Urn 2:
| Urn 1 | Urn 2 | |
|---|---|---|
| Probability of drawing a white ball | 0.6 | 0.6 |
| Probability of drawing a yellow ball | 0.4 | 0.4 |
As can be seen from the table, the probabilities of drawing white or yellow balls from Urn 1 are equal to those of Urn 2.
Applications
The concepts of probability and conditional probability have numerous applications in real-world scenarios, including:
- Predicting outcomes in games of chance, such as lotteries or card games.
- Evaluating the risk of events, such as accidents or illnesses.
- Making informed decisions based on the likelihood of various outcomes.
FAQ Guide
What is the probability of drawing a white ball from the first urn?
The probability depends on the specific distribution of balls in the urn, which is not provided in the given Artikel.
How does conditional probability affect the analysis?
Conditional probability considers the outcome of a previous draw, influencing the probability of subsequent draws. This concept plays a crucial role in understanding the relationships between the urns and the colors of balls drawn.

