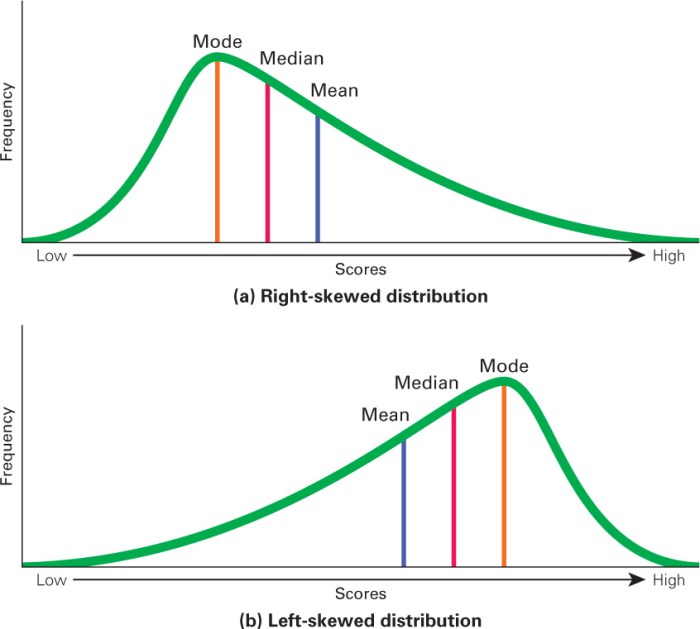
Which of the following depicts a moderately left-skewed distribution? This question delves into the fascinating realm of data analysis, where understanding the characteristics and implications of skewness is crucial. Skewness, a measure of asymmetry in data distribution, plays a significant role in shaping the interpretation and modeling of statistical data.
In this exploration, we will embark on a journey to define moderately left-skewed distributions, unravel their distinctive features, and uncover the methods employed to identify and assess skewness. Through real-world examples and data visualization techniques, we will illuminate the practical implications of skewness and provide guidance on how to adjust for its effects in data analysis.
Understanding Skewness
Skewness mengacu pada asimetri dalam distribusi data. Ini mengukur seberapa jauh distribusi data menyimpang dari distribusi normal yang simetris. Distribusi dapat menunjukkan skewness positif (kanan) atau negatif (kiri), tergantung pada arah penyimpangan.
Skewness penting dalam analisis data karena dapat memengaruhi interpretasi hasil statistik. Misalnya, rata-rata mungkin bukan ukuran pusat yang representatif untuk distribusi yang sangat miring.
Characteristics of Moderately Left-Skewed Distribution
Distribusi yang agak miring ke kiri memiliki karakteristik berikut:
- Kurva distribusi menumpuk di sisi kanan.
- Ekor distribusi lebih panjang di sisi kiri daripada di sisi kanan.
- Median lebih kecil dari mean.
Outlier dapat memengaruhi skewness, terutama pada distribusi yang kecil. Outlier di sisi kiri dapat membuat distribusi tampak lebih miring ke kiri, sementara outlier di sisi kanan dapat mengurangi skewness.
Methods for Identifying Skewness, Which of the following depicts a moderately left-skewed distribution
Skewness dapat diidentifikasi menggunakan metode grafis dan numerik:
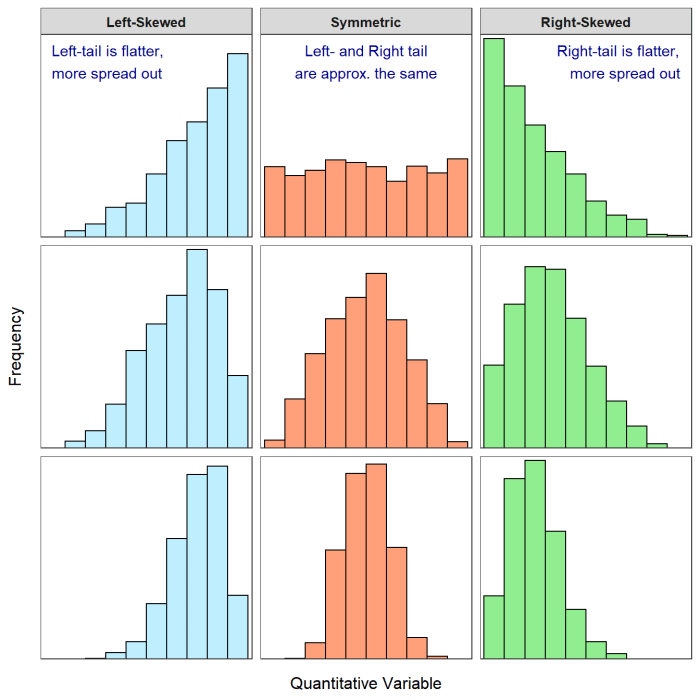
- Histogram:Histogram menunjukkan bentuk distribusi dan asimetrinya.
- Box Plot:Box plot menampilkan median, kuartil, dan outlier, memberikan gambaran visual tentang skewness.
- Skewness Coefficient:Koefisien skewness adalah ukuran numerik skewness, dengan nilai positif menunjukkan skewness ke kanan dan nilai negatif menunjukkan skewness ke kiri.
Examples of Moderately Left-Skewed Distributions
Distribusi miring ke kiri yang umum meliputi:
- Distribusi penghasilan, di mana sebagian besar orang berpenghasilan rendah dan hanya sedikit orang berpenghasilan sangat tinggi.
- Distribusi waktu tunggu, di mana sebagian besar waktu tunggu singkat dan hanya sedikit waktu tunggu yang sangat lama.
Implications of Skewness
Skewness dapat memengaruhi analisis statistik dengan cara berikut:
- Pengaruh pada Mean:Mean dapat terpengaruh oleh outlier dan skewness, sehingga tidak selalu menjadi ukuran pusat yang representatif.
- Pengaruh pada Regresi:Skewness dapat memengaruhi kemiringan garis regresi, yang dapat menyebabkan kesimpulan yang menyesatkan.
Untuk menyesuaikan skewness, transformasi data dapat digunakan untuk menormalkan distribusi, seperti transformasi log atau akar kuadrat.
Helpful Answers: Which Of The Following Depicts A Moderately Left-skewed Distribution
What is skewness?
Skewness measures the asymmetry of a data distribution around its mean. Positive skewness indicates a longer tail on the right side of the distribution, while negative skewness indicates a longer tail on the left side.
How do you identify a moderately left-skewed distribution?
A moderately left-skewed distribution has a mean that is shifted to the right of the median, a longer tail on the left side, and a skewness coefficient between -1 and 0.
What are the implications of skewness in data analysis?
Skewness can affect the validity of statistical tests, the accuracy of parameter estimation, and the interpretation of results. It is important to consider skewness when drawing conclusions from data.